Ti sarà sicuramente capitato di dover risolvere un problema di geometria…e di dimenticare qualche formula! Vero? Questo accade poiché spesso e volentieri questo è un problema di approccio. Se vuoi dimenticare qualcosa, sicuramente quello che devi fare è impararla a memoria! Il consiglio che do a tutti i miei studenti è quello di capire il ragionamento e solo dopo imparare una formula. Partiamo dal principio.
Che differenza c’è tra un quadrato ed un cubo?
La stessa che c’è tra questi videogiochi di Super Mario della Nintendo:


La stessa che c’è tra questi due giochi di Super Mario!
A sinistra, troviamo uno dei primi giochi di Super Mario in due dimensioni: questo è il quadrato.
A destra, troviamo uno degli ultimi giochi di Super Mario: questo è in tre dimensioni! I personaggi hanno un…volume!
Il vecchio gioco di Super Mario ha dei personaggi che sono lunghi ed alti, ma non sono profondi! A differenza del secondo gioco, in cui i personaggi hanno una profondità!
Il volume del cubo
Cos’è il volume? Il volume misura quanto spazio occupa un oggetto tridimensionale.
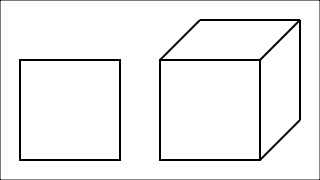
Come abbiamo visto, le tre dimensioni sono: lunghezza, altezza ed profondità. La terza dimensione, che un cubo ha rispetto ad un quadrato è proprio la profondità. Un quadrato puoi disegnarlo su di un foglio di carta e poggiarlo sul pavimento. Non ha una altezza!
Invece, su di un cubo ti ci puoi sedere perché è alto.
Quanto è lungo un cubo? Quanto è largo un cubo? Quanto è alto un cubo?
Guarda il seguente cubo, e dimmi cosa osservi.

Esatto! Lunghezza, larghezza ed altezza sono tutte uguali al lato l del quadrato.
Quindi:
V = l^3
oppure
La superficie totale del cubo
Immaginiamo un dado, quello che usiamo per giocare. Ogni faccia del dado è uguale alle altre, giusto? Se vogliamo scoprire quanta “carta regalo” ci vuole per coprire tutto il dado, stiamo cercando la sua superficie totale.
Ogni faccia del dado è un quadrato perfetto. Se chiamiamo l la lunghezza del lato di questo quadrato, possiamo dire che lo spazio che una faccia occupa su un tavolo è l moltiplicato per l :
Area\ di\ una\ faccia = l \times lMa il dado ha 6 facce, tutte uguali. Quindi, per trovare quanto spazio occupano tutte le facce messe insieme, dobbiamo prendere l’area di una faccia e moltiplicarla per 6:
Superficie\ totale = 6 \times (l \times l)In parole semplici, moltiplichiamo la lunghezza del lato del quadrato per se stessa (questo ci dà l’area di una faccia) e poi moltiplichiamo quel numero per 6 (perché abbiamo 6 facce uguali sul dado). Questo ci dà la superficie totale del dado.
Questo modo di fare ci aiuta a capire quanto “carta da regalo” ci servirebbe se volessimo incartare completamente il dado. Semplice, no?
Osserva le sei facce del cubo:






















What do you think?
It is nice to know your opinion. Leave a comment.