Cosa sai dirmi sui quadrilateri? L’articolo definitivo che li sintetizza al meglio

24 February 2024Geometria piana, Matematica

Cosa sai dirmi sui quadrilateri? L’articolo definitivo che li sintetizza al meglio

Confessa: ti è capitato, almeno una volta, di non saper rispondere ad una domanda sulle aree delle figure o sul perimetro delle figure. Oppure di non riuscire a descrivere le varie figure geometriche con precisione. Da insegnante, questo è uno degli argomenti più temuti. Da oggi, non sarà più così.

Devi solo imparare ad osservare le figure

Qui sotto, troverai una tabella che io definisco “magica”. Tutti i quadrilateri (figure che hanno quattro lati e quattro angoli) seppur siano diversi, hanno qualcosa in comune. Ti riporto la tabella con le figure:

Nome	Lati	Angoli	Formula dell’Area	Formula del Perimetro
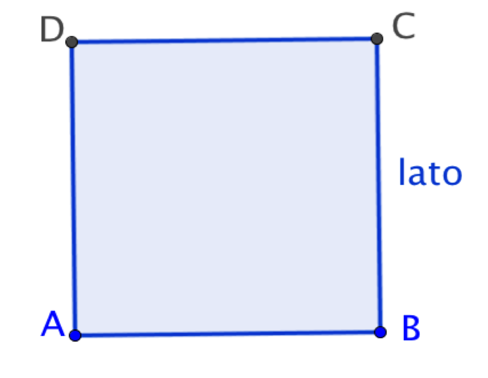Quadrato	Tutti uguali	Tutti uguali (90°)	$\text{A} = l*l$	$\text{p} = 4 \cdot l$
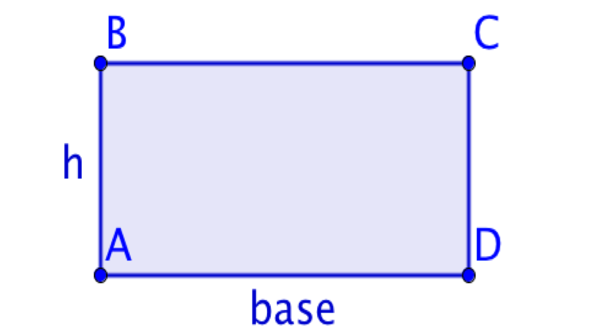Rettangolo	Uguali a due a due (quelli opposti)	Tutti uguali (90°)	$\text{A} = b \cdot h$	$\text{p} = (2 \cdot b) +(2 \cdot h)$
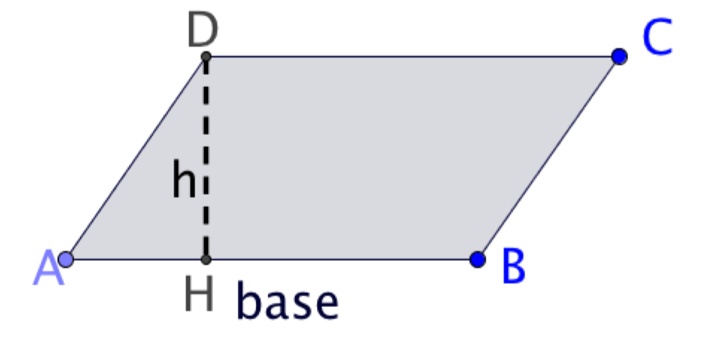Parallelogrammo	Uguali a due a due (quelli opposti)	Uguali a due a due (quelli opposti)	$\text{A} = b \cdot h$	$\text{p} = (2 \cdot b) +(2 \cdot l)$
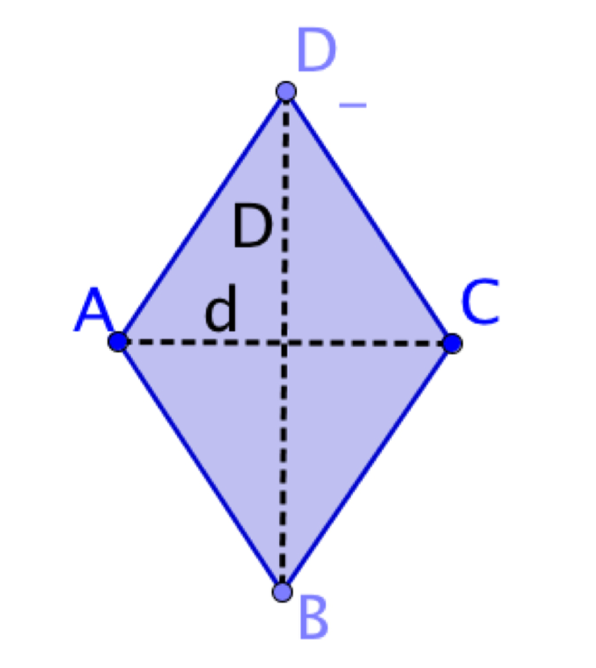Rombo	Tutti uguali	Uguali a due a due (quelli opposti)	$\text{A} = \frac{d_1 \cdot d_2}{2}$	$\text{p} = 4 \cdot l$

Dico sempre ai miei ragazzi, che le risposte spesso e volentieri sono nelle domande. Osserviamo la tabella: tutti uguali ed uguali a due a due sono delle espressioni che si ripetono per tutte le figure che ho elencato qui sopra. Proviamo a ragionarci su, osservando una figura alla volta.

Il quadrato

Proviamo ad osservare il quadrato! I lati del quadrato sono tutti uguali, ed i suoi angoli sono tutti uguali e misurano 90°. E’ stato facile vero?

Sai cos’è il perimetro? Bravo, la somma di tutti i lati! Allora se i lati del quadrato sono 4, ed i lati sono tutti uguali…l’area del quadrato è lato * 4! Quindi= $\text{p} = 4 \cdot l$ .
E’ stato semplice vero?

Come faccio a capire cos’è l’area del quadrato? Hai presente come funziona una fotocopiatrice? C’è un raggio luminoso che illumina tutta la superficie del vetro. Ora, immagina di avere una fotocopiatrice rettangolare. La barra luminosa si muove lungo tutto il vetro fino ad illuminarlo per intero. Chiamiamo la barra luminosa “L”, come il lato del nostro quadrato. Per illuminare tutto il vetro, questa barra si deve muovere lungo tutto l’altro lato, che misura sempre “L”. Quindi un lato luminoso “L”, scivola lungo tutto l’altro lato…che misura sempre “L”. Da qui la formula: $\text{A} = l*l$ .

Il rettangolo

Proviamo ad osservare il il rettangolo. I lati del quadrato sono uguali a due a due (quelli opposti), ed i suoi angoli sono tutti uguali e misurano 90°. Noti come possiamo descrivere tutte queste figure in questi termini?

Se i lati sono uguali due a due, significa che abbiamo due basi uguali e due altezze uguali che possiamo sommare tra loro per trovare il perimetro: $\text{p} = (2 \cdot b) +(2 \cdot h)$ .

Per l’area del rettangolo invece? Possiamo usare un analogo concetto di “illuminazione” come abbiamo fatto con il quadrato. Immagina ancora la fotocopiatrice rettangolare: stavolta la barra luminosa, che chiameremo sempre “B” (base), si muove lungo l’altezza “H“. Quindi la formula dell’area sarà: $\text{A} = b \cdot h$ .

Il parallelogrammo

Proviamo ad osservare il il rettangolo. I lati del quadrato sono uguali a due a due (quelli opposti), ed anche i suoi angoli sono uguali a due a due (quelli opposti). Osserviamo gli angoli nel vertice A e nel vertice C: sono acuti e congruenti (cioè uguali). Gli angoli nel vertice D e B sono invece ottusi e congruenti.

Se i lati sono uguali due a due, significa che abbiamo due basi uguali e due lati obligui uguali che possiamo sommare tra loro per trovare il perimetro: $\text{p} = (2 \cdot b) +(2 \cdot l)$ .

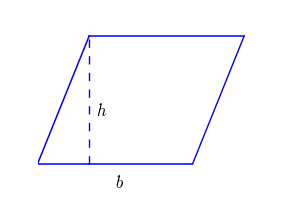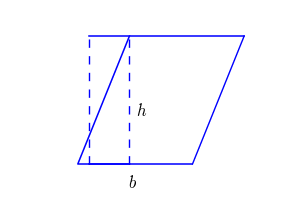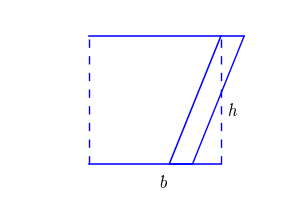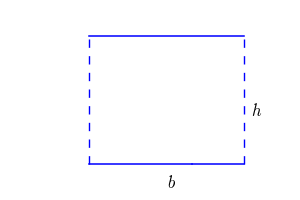
E l’area del parallelogrammo? Guarda l’immagine a destra: spostando quel triangolo rettangolo…il parallelogrammo diventa un rettangolo! Quindi la formula dell’area sarà identica a quella del rettangolo: $\text{A} = b \cdot h$ .

FAI ATTENZIONE: L’altezza, nel rettangolo, coincide con il lato, mentre nel parallelogrammo non coincide con il lato.

Il rombo

Proviamo ad osservare il rombo! I lati del quadrato sono tutti uguali, ed i suoi angoli sono uguali a due a due (quelli opposti). Osserviamo gli angoli nel vertice D e nel vertice B: sono acuti e congruenti (cioè uguali). Gli angoli nel vertice A e D sono invece ottusi e congruenti. (Ti ricorda qualcosa???)

Se i lati sono tutti uguali e sono 4, allora il perimetro sarà: $\text{p} = 4 \cdot l$ .

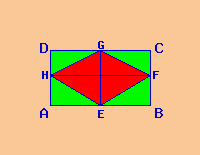
L’area del rombo? Osserva l’immagine a destra: c’è un rombo in un triangolo rettangolo. La base del rettangolo (AB) coincide con la diagonale maggiore del rombo (HF), mentre l’altezza del rettangolo (DA) coincide con la sua diagonale minore (GE). Quindi, se facessimo $Base \cdot Altezza$ del rettangolo (Cioè $Diagonale maggiore \cdot Diagonale minore$ ), otterremmo l’area del rettangolo che è il doppio di quella del rombo. Quindi: $\text{p} = 4 \cdot l$ .

Il trapezio

Per il trapezio, invece, ti propongo uno schema sintetico da imparare a memoria. Purtroppo, esistendo diversi tipi di trapezi, gli angoli ed i lati cambiano molto! Per questo ti consiglio di osservare attentamente le figure ed imparare le informazioni guardando la figura.

Nome	Lati	Angoli	Formula dell’Area	Formula del Perimetro
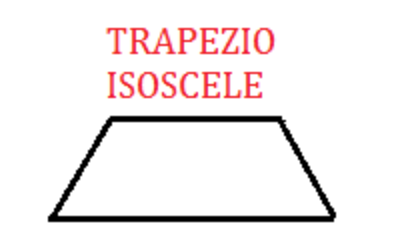Trapezio Isoscele	Due lati uguali (non paralleli)	Due angoli alla base uguali	$\text{A} = \frac{(B + b) \cdot h}{2}$	$\text{p} = B + b + 2 \cdot l$
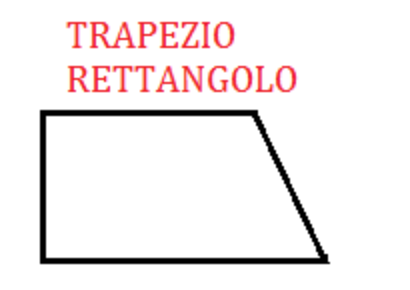Trapezio Rettangolo	Due lati paralleli, uno perpendicolare alle basi	Due angoli retti	$\text{A} = \frac{(B + b) \cdot h}{2}$	$\text{p} = B + b + l_1 + l_2$
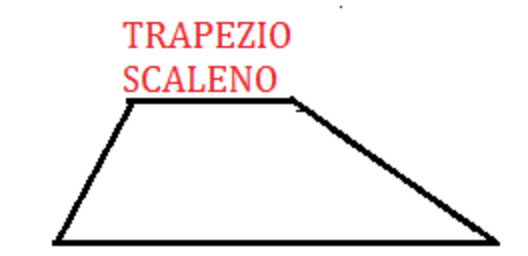Trapezio Scaleno	Nessun lato uguali	Angoli di diversa misura	$\text{A} = \frac{(B + b) \cdot h}{2}$	$\text{p} = B + b + l_1 + l_2$