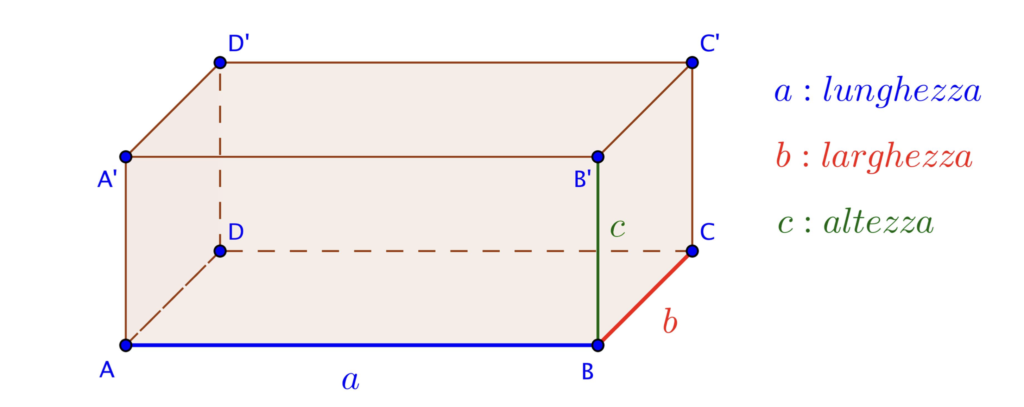
Immagine una scatola di scarpe, un mattone, il vostro libro di matematica chiuso od un edificio. Questi oggetti hanno tutti una forma comune: sono parallelepipedi rettangoli. Ma cosa significa esattamente?

Un parallelepipedo rettangolo è un solido a sei facce, dove:

• ogni faccia è un rettangolo;
• tutti gli angoli sono angoli retti (90 gradi).

La superficie della scatola

Osserviamo i sei rettangoli (quelli che vediamo e non vediamo) dell’immagine precedente.
Sono tutti uguali, oppure no?
Guardando l’immagine, notiamo che i rettangoli sono diversi, anche se…alcuni di loro sono uguali!

Immaginiamo di essere in una scatola, come i bambini alla nostra destra. Allo stesso tempo, guardati intorno nella stanza in cui ti trovi, noterai che il pavimento ed il soffitto hanno una stessa superficie.

Rivestiamo il pavimento ed il soffitto

Adesso immaginiamo di voler fare una magia e rivestire con della carta regalo il pavimento ed il soffitto della nostra scatola: di quanta carta avremmo bisogno?

Per fare questo calcolo, ci basterà trovare l’area del pavimento (dato che il soffitto è uguale).
Essendo il pavimento un rettangolo, l’area la calcoleremo:

Area \, base= lunghezza * larghezza

La base e l’altezza del rettangolo corrisponderanno alla lunghezza ed alla larghezza della nostra scatola, cioè alla lunghezza e la larghezza del nostro parallelepipedo rettangolo!

Rivestiamo le pareti della scatola

Allora, immaginiamo di voler avvolgere magicamente le pareti laterali della nostra scatola con della carta colorata. La domanda sorge spontanea: quanta carta ci servirebbe per questo incantesimo?

Per rispondere, concentriamoci su un dettaglio cruciale: le informazioni sul rettangolo di base della nostra scatola. Il segreto sta nel perimetro di questo rettangolo, che ci aprirà la porta verso la conoscenza dell’area laterale del parallelepipedo.

Ecco come possiamo procedere: calcoliamo prima il perimetro della base della scatola. Se pensiamo alla base come a un rettangolo, il suo perimetro si ottiene:

\text{perimetro} = (2 \cdot base rettangolo) +(2 \cdot altezza rettangolo)

Ora, per scoprire di quanta carta abbiamo bisogno per rivestire le pareti laterali, dobbiamo semplicemente moltiplicare il perimetro della base per l’altezza h della scatola. Questo perché l’altezza delle pareti laterali si estende verticalmente dalla base, e il perimetro ci dà la misura lineare che circonda la base. Quindi, l’area laterale:

\text{A \, lat} = [(2 \cdot lunghezza) +(2 \cdot larghezza)]* altezza

Questa formula è il tuo passaporto per calcolare esattamente l’area necessaria a rivestire le pareti laterali della scatola, trasformando un semplice parallelepipedo in un oggetto di puro fascino e bellezza.

Come si calcola l’area totale della scatola?

Per calcolare quanta carta ci serve per rivestire tutta la scatola, ci basterà sommare la carta che ci serve per rivestire il pavimento ed il soffitto, alla carta che ci serve per rivestire le pareti della scatola, per un totale di 6 facce!

AREA TOTALE PARALLELEPIPEDO RETTANGOLO

\text{A \, totale} = 2 * Area \, base * Area \, laterale

\text{A \, laterale} = [(2 \cdot lunghezza) +(2 \cdot larghezza)]* altezza

Come si calcola il volume del parallelepipedo rettangolo?

Immaginiamo adesso di voler scoprire quanto è grande all’interno la nostra scatola, non misurando quanto spazio occupa sul tavolo o quanto è alto, ma quanto può contenere dentro di sé.
Questa curiosità ci porta a esplorare il concetto di volume.

Pensate al volume come alla quantità di acqua che potreste versare all’interno del parallelepipedo fino a riempirlo completamente, senza lasciare spazio vuoto. Questa quantità di acqua, o di qualsiasi altra cosa decidiate di riempirlo, rappresenta il volume del nostro parallelepipedo rettangolo.

Ma come facciamo a calcolare esattamente quanto può contenere, senza dover effettivamente riempire il parallelepipedo con dell’acqua? Qui entra in gioco la matematica, con una semplice ma potente formula:

Volume= lunghezza * larghezza * altezza

Ogni dimensione del parallelepipedo rettangolo contribuisce a determinare quanto spazio c’è all’interno. La lunghezza è quanto è lungo il parallelepipedo da una parte all’altra; la larghezza è quanto è ampio; e l’altezza è quanto è alto dal basso verso l’alto.

Per esempio, se avete un parallelepipedo rettangolo con una lunghezza di 5 metri, una larghezza di 2 metri e un’altezza di 3 metri, il suo volume sarà:

Volume= 5 * 2 * 3 = 30 \, metri \, cubi